Cet article est le trente-huitième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le trente-septième, j’ai expliqué ce qu’était la forme logique des propositions. Dans cet article, je présenterai les diagrammes d’Euler. Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft des pages 152 à 153. Pour aller plus loin (sur les diagrammes de Venn, plus de schémas et sur les limites des diagrammes d’Euler), on pourra consulter cet article dont j’ai repris quelques images.

Les diagrammes d’Euler sont des représentations graphiques qui permettent de visualiser les relations entre plusieurs groupes. Ils sont surtout utilisés avec les diagrammes de Venn en mathématiques¹: on appelle alors les groupes ensembles. Mais ils peuvent aussi servir dans les raisonnements de la vie de tous les jours grâce à leur aspect intuitif. En logique aristotélicienne, ils servent :

1. à mieux comprendre ce que disent les propositions et
2. à vérifier rapidement et facilement si un syllogisme² est valide.

Un exemple de diagramme d’Euler

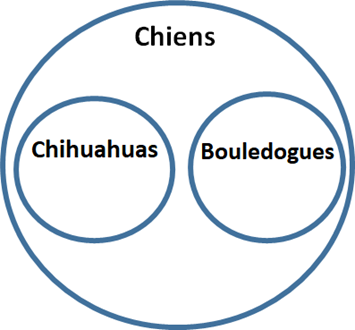
Dans cet exemple, on voit trois cercles qui représentent trois groupes. Un grand cercle 1 qui représente le groupe des chiens qui contient deux petits cercles qui représentent respectivement le groupe des chihuahuas (cercle 2) et le groupe des bouledogues (cercle 3).

Cela nous permet de savoir que le groupe des chiens est un groupe général qui contient deux races³, celle des chihuahuas et celle des bouledogues.

Autrement dit, tout chihuahua est un chien, tout bouledogue est un chien. Un chien n’est pas forcément un chihuahua, ni forcément un bouledogue.

On peut bien évidemment généraliser cet exemple en remplaçant le nom de ces groupes par n’importe quels autres groupes. De manière abstraite, on peut même donner des noms de groupes généraux comme on le fait traditionnellement avec des lettres en majuscules :

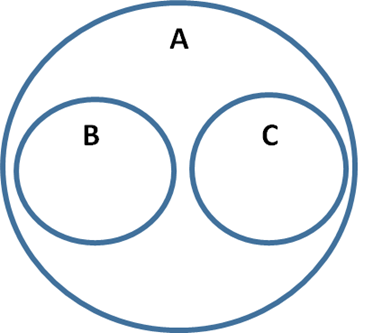
Les diagrammes d’Euler des quatre formes logiques

On peut également représenter⁴ nos quatre propositions catégoriques (A, I, E, O). Je ferai en passant quelques rappels sur ces propositions que nous avons étudiées dans l’article précédent. S est le sujet (ce à quoi on attribue un prédicat) d’une proposition et P son prédicat (une caractéristique).

1. Diagramme d’Euler de A (des propositions universelles affirmatives)

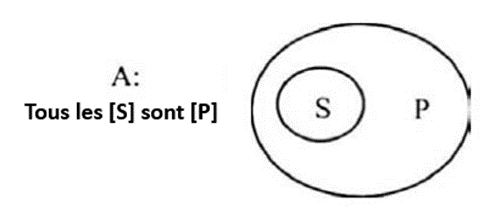
La proposition A (universelle affirmative) affirme que tout S est P (par exemple « Tous les hommes sont mortels. »). En termes de compréhension, P fait partie de la définition de S. En termes d’extension, la population de S appartient celle de P⁵. On représente cela dans le diagramme d’Euler en dessinant le cercle S (qui représente le sujet) à l’intérieur du cercle P (qui représente le prédicat).

2. Diagramme d’Euler de E (des propositions universelles négatives)

La proposition E (universelle négative) affirme qu’aucun S n’est P⁶ (par exemple « Aucun homme n’est mortel. »). En termes de compréhension, P ne fait pas partie de la définition de S. En termes d’extension, la population de S et celle de P n’ont aucun « habitant » en commun⁷. On représente cela dans le diagramme d’Euler en dessinant deux cercles S et P qui s’excluent, qui ne se coupent en aucune zone.

3. Diagramme d’Euler de I (des propositions particulières affirmatives)

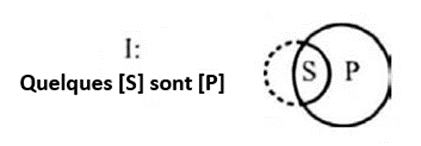
La proposition I (particulière affirmative) affirme que quelques S sont P (par exemple « Quelques hommes sont mortels. »). En termes de compréhension, P fait partie de la définition de quelques S (mais pas tous). En termes d’extension, une partie de la population de S (mais pas toute) appartient celle de P.

On représente cela dans le diagramme d’Euler en dessinant un endroit commun entre le cercle S et cercle P avec des pointillés pour son côté gauche (côté vers S). Les pointillés du côté gauche indiquent qu’on ne sait pas combien de S ne sont pas P. En effet, étant donné le sens imprécis de « quelques » dans « quelques S sont P », on est sûr qu’il y a certains S qui sont P (côté droit avec des traits pleins) mais on ne sait pas combien de S ne sont pas P (côté gauche avec des traits en pointillés). Plusieurs cas (1, 2, 3, 10 d’entre eux, tous ?) sont possibles.

4. Diagramme d’Euler de O (des propositions particulières négatives)

La proposition O (particulière négative) affirme quelques S ne sont pas P (par exemple « Quelques hommes ne sont pas mortels. »). Attention à une ambiguïté ! On rappelle que dedans, « quelques » est à prendre au sens de « aux moins certains, quelques-uns » (un sens faible) et non pas au sens de « seulement certains, mais pas tous » (un sens fort). En termes de compréhension, P fait partie de la définition de S. En termes d’extension, la population de S appartient celle de P.

On représente cela dans le diagramme d’Euler en dessinant un endroit commun entre le cercle S et cercle P avec des pointillés pour son côté droit (côté vers P). Les pointillés du côté droit indiquent qu’on ne sait pas combien de S sont P. En effet, étant donné le sens imprécis de « quelques » dans « quelques S ne sont pas P », on est sûr qu’il y a certains S qui ne sont pas P (côté gauche avec des traits pleins) mais on ne sait pas combien de S sont P (côté droit avec des traits en pointillés). Plusieurs cas (1, 2, 3, 10 d’entre eux, tous ?) sont possibles.

Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants illustres – Savants de l’antiquité (tome 1), Paris, 1866, pp. 134-135.

1. On est alors en logique moderne ou mathématique, où on cherche à tout quantifier.[↩]
2. Un type d’argument fondamental qu’on étudiera par la suite en long, en large et en travers.[↩]
3. Et bien sûr de nombreux autres groupes qu’on n’a pas représentés par manque de place : celui des bergers allemands, celui des cockers, etc.[↩]
4. J’ai repris les schémas de Kreeft, pp. 152-153.[↩]
5. On dira que l’ensemble S est inclus dans l’ensemble P.[↩]
6. On a choisi cette formulation pour éviter l’ambiguïté qui apparaîtrait si l’on disait plutôt « Tous les [S] ne sont pas [P] ».[↩]
7. Pour les matheux, on dira que l’intersection des ensembles S et P est vide.[↩]