Cet article est le quarantième-sixième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le quarante–cinquième, j’ai présenté les contradictions. Dans cet article, j’expliquerai ce que sont les différents types d’oppositions à travers un schéma classique depuis l’Antiquité : le carré des oppositions. Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft des pages 173-178.

Dans l’article précédent, nous avons étudié les contradictions. Celles-ci sont en fait un cas particulier des oppositions. Une opposition est la relation entre deux propositions (une affirmation et une négation) qui ont le même sujet et le même prédicat mais qui diffèrent en qualité (affirmation ou négation), en quantité (universel ou particulier) ou en les deux.

Nous allons voir dans la suite les différents types d’oppositions à l’aide d’un schéma appelé traditionnellement le carré des oppositions. On le retrouve souvent chez les philosophes scolastiques (du Moyen Âge) qui l’ont eux-mêmes repris d’Aristote et de Boèce.

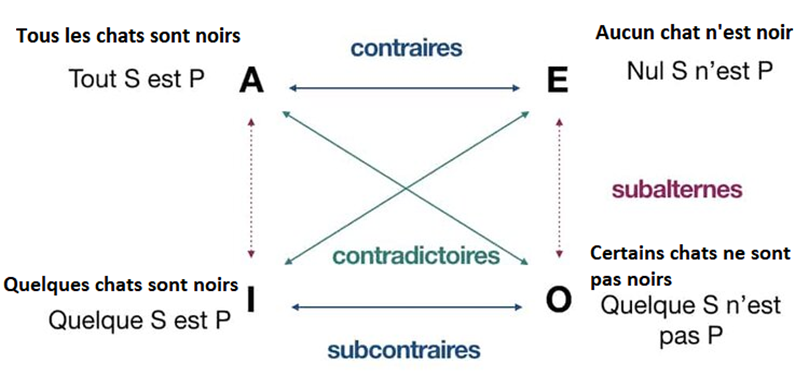
Je rappelle les notations A, E, I et O :

A : La proposition universelle affirmative
E : La proposition universelle négative
I : La proposition particulière affirmative
O : La proposition particulière négative.

Chaque flèche représente un type d’opposition bien précis. On en distingue quatre en tout :

1. L’opposition contradictoire (ou des propositions contradictoires)
2. L’opposition contraire (ou des propositions contraires)
3. L’opposition subcontraire ou sous-contraire (ou des propositions sous-contraires)
4. L’opposition subalterne ou subordonnée (ou des propositions subalternes)

Je reprends ici pour chaque type d’opposition les définitions et les règles claires et concises du manuel de logique d’Arthur Robert (gratuit en ligne).

Les quatre types d’opposition

1. L’opposition contradictoire (propositions contradictoires)

L’opposition contradictoire est celle qui existe entre deux propositions dont l’une est universelle, l’autre particulière, l’une affirmative, l’autre négative. Ex. : Tous les anges sont des êtres spirituels. Quelques anges ne sont pas des êtres spirituels. Les contradictoires s’opposent donc quantitativement et qualitativement.

Arthur Robert, Leçons de logique, Québec : Action Sociale limitée, 1915, [1^re éd. 1914], p. 31.

Deux contradictoires ne peuvent pas être à la fois vraies ou fausses, si l’une est vraie, l’autre est fausse, et réciproquement. S’il est vrai que tout homme est sage (A), il est donc faux que quelque homme n’est pas sage (O). Dans deux contradictoires l’une est toujours la négation de l’autre.

Ibid., pp. 32-33.

2.      L’opposition contraire (propositions contraires)

L’opposition contraire est celle qui existe entre deux propositions universelles dont l’une est affirmative et l’autre négative. Ex. : Toutes les âmes humaines sont immortelles. Toutes les âmes humaines ne sont pas immortelles. Les propositions contraires sont opposées qualitativement.

Ibid., p. 31.

Deux contraires ne peuvent être vraies à la fois, mais elles peuvent être fausses. Si tout homme est sage (A) il est faux de dire qu’aucun homme n’est sage (E). Mais en supposant qu’il soit faux d’affirmer que tout homme est sage, il peut être aussi faux d’affirmer qu’aucun homme n’est sage (E). En effet, du moment qu’on nie la sagesse à tous les hommes, il ne s’ensuit pas nécessairement que personne ne la possède. Quelques-uns peuvent l’avoir.

Ibid., p. 33.

3.      L’opposition sous-contraire ou subcontraire (propositions sous-contraires)

L’opposition sous-contraire est celle qui existe entre deux propositions particulières dont l’une est affirmative et l’autre négative. Ex. : Quelques hommes sont instruits. Quelques hommes ne sont pas instruits. Les sous-contraires diffèrent entre elles par la qualité.

Ibid., p. 31.

Deux sous-contraires ne peuvent pas être fausses à la fois, mais elles peuvent être vraies. Il est vrai de dire que quelque homme est sage (I) et n’est pas sage (O), parce qu’il n’est pas question du même homme. Mais s’il est faux de dire que quelque homme est sage (I), il s’ensuit que la proposition : Quelque homme n’est pas sage (O) est vraie.

Ibid., p. 33.

4. L’opposition subalterne ou subordonnée (propositions subalternes)

L’opposition subalterne est celle qui existe entre deux propositions dont l’une est universelle et l’autre particulière. Les subalternes diffèrent par la quantité. Ex. : Tous les hommes sont sages — Quelques hommes sont sages. Aucun homme n’est sage — Quelque homme n’est pas sage.

Ibid., p. 32.

Une version du carré logique plus utile et facile à retenir

Au lieu d’apprendre par cœur le carré logique ci-dessus avec toutes ses règles pour chaque type opposition, on peut apprendre celui-ci qui servira beaucoup en pratique :

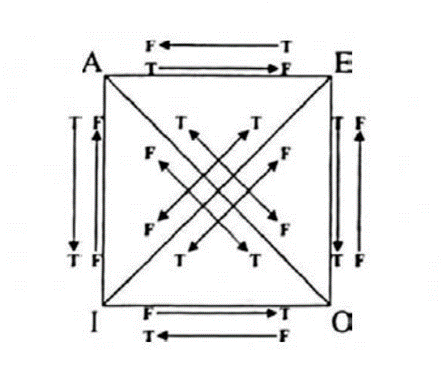
Règles de lecture

Pour le comprendre, il faut juste savoir que

1. Chaque flèche représente une inférence valide.
2. Le point de départ de la flèche représente la prémisse.
3. Le point d’arrivée de la flèche représente la conclusion.
4. S’il n’y a pas de flèche entre deux propositions, cela veut dire qu’il n’y a pas d’inférence valide, que si on fait une inférence, elle sera invalide.
5. T et F veulent dire vrai et faux (T pour true et F pour false en anglais).

Par exemple, la flèche tout en haut de E vers A (F <= T) représente l’inférence d’une proposition E (la prémisse = le point de départ de la flèche) vers une proposition A (la conclusion = le point d’arrivée de la flèche). Concrètement, cela signifie que si on sait qu’une proposition E est vraie, alors on peut en déduire qu’une proposition A (ici c’est la proposition contraire de E) est fausse.

À quoi sert ce nouveau schéma ?

Il nous permet d’apprendre deux choses :

1. Il nous apprend quelles propositions se contredisent (en regardant les flèches sur la diagonale).
   Ce qui est utile pour savoir quelle proposition on a besoin de prouver pour en réfuter une autre. Par exemple, pour réfuter « Tous les chats sont noirs » (A), le schéma me dit (flèche en diagonale de A vers O) que je devrais prouver que « Certains chats ne sont pas noirs. » (O)
2. Il nous apprend quelles inférences entre deux propositions opposées sont valides ou invalides.
   Toutes les inférences représentées sont valides. À l’inverse, toute inférence qui n’est pas représentée sur le schéma est invalide. Par exemple, je sais que l’inférence E vraie vers A fausse est valide car elle est bien représentée. Mais ce n’est pas le cas de l’inférence E fausse vers A vraie, donc celle-ci est invalide.

Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants i

1. Je me suis permis de rajouter les exemples avec les chats noirs.[↩]