Cet article est le cinquante-huitième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le cinquante–septième, j’ai présenté la méthode socratique, une méthode de Socrate qui combine déductions et inductions pour parvenir à une conclusion certaine. Dans cet article, je ferai une introduction du syllogisme en présentant sa structure et sa stratégie. Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft, pp. 215-218.

La structure du syllogisme

Le syllogisme n’est rien d’autre que le cœur la logique, le nerf de la guerre comme l’on dit. C’est un type d’argument très naturel, facile à maîtriser et convaincant. Par exemple :

1. Tous les hommes sont mortels.
2. Socrate est un homme.
3. Donc Socrate est mortel.

Voici ses différentes composantes avec leur nom technique¹:

• Il y a trois propositions : deux prémisses (qui constituent l’antécédent) et une seule conclusion (aussi appelée le conséquent).
• Il y a trois termes qui sont chacun utilisés deux fois.
• Le sujet de la conclusion s’appelle petit terme (parfois petit extrême).
• Le prédicat de la conclusion s’appelle grand terme (parfois grand extrême).
• Le terme qui apparaît dans chaque prémisse mais pas dans la conclusion s’appelle moyen terme.
• La prémisse qui contient le grand terme s’appelle la majeure.
• La prémisse qui contient le petit terme s’appelle la mineure.
• Même si en général on place la majeure avant la mineure, il n’y a pas d’ordre à respecter à part mettre la conclusion en dernière place.

On peut résumer tout cela avec notre éternel exemple par ce schéma :

Voici les notations utilisées dans le schéma et qu’on reprendra pour gagner du temps :

• S = le petit terme (S parce que c’est le sujet de la conclusion)
• P = le grand terme (P parce que c’est le prédicat de la conclusion)
• M = le moyen terme (M pour « moyen » terme)

En pratique, comment les identifier dans un raisonnement ?

1. Trouver la conclusion.
2. Trouver le petit terme et le grand terme : ils sont respectivement le sujet et le prédicat de la conclusion.
3. Trouver la majeure et la mineure : elles contiennent respectivement le grand terme et le petit terme.
4. Trouver le moyen terme : c’est celui qui reste et qui ne se trouve pas dans la conclusion mais dans chaque prémisse.

Pour finir, quelques remarques :

• Dans un syllogisme sous sa forme logique, on place souvent par convention la prémisse majeure en premier puis la mineure et enfin la conclusion. Mais dans nos discussions de tous les jours, l’ordre n’a pas d’importance.
• On a même l’habitude d’omettre l’une des deux prémisses car on suppose que tout le monde l’a en tête et qu’il est donc inutile de la mentionner explicitement. C’est ce qu’on appelle un enthymème qui vient du grec « garder en tête ».
• La seule règle cruciale est de faire dépendre la conclusion des prémisses avec des mots clés comme « donc », « parce que », « en effet », etc.

La stratégie du syllogisme

Pour comprendre la « stratégie » qu’emploie le syllogisme pour prouver sa conclusion, on peut observer et étudier ce schéma :

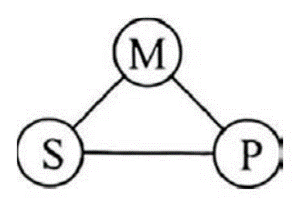
Le but est de prouver dans la conclusion (à propos de S et P où S est le sujet et P le prédicat) :

1. Soit que le prédicat P (par exemple : gentil) peut être affirmé à propos du sujet S (par exemple : Laurent)
2. Soit que le prédicat P (par exemple : gentil) ne peut pas être affirmé à propos du sujet S (par exemple : Laurent)

Pour cela, nous relions S et P à un troisième même terme M (le moyen terme). Voici quelques comparaisons pour comprendre :

• M est la pierre angulaire du syllogisme (ce qui le fait tenir debout) : on rattache S et P à M pour savoir s’ils vont ensemble ou non.
• Tout comme on teste si deux aimants ont des pôles de polarité différentes en les faisant interagir avec un troisième aimant, on rattache S et P à M.
• M est le milieu du pont qui relie les deux extrémités S et P. La liaison de S à M (la prémisse majeure) et celle de M à P (la prémisse mineure) forment les deux moitiés du pont. La stabilité du pont dépend ultimement du milieu M.

Etudions maintenant les trois différents cas possibles.

Le syllogisme avec une conclusion affirmative

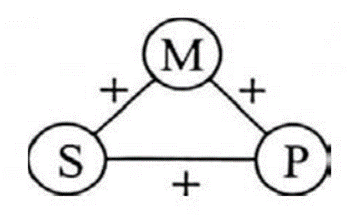
Dans ce cas, M est relié à S et à P à chaque fois dans une prémisse qui est une proposition affirmative (de la forme « x est y ») : « S est M » et « M est P ». On a alors que S doit être relié à P dans une conclusion affirmative : « S est P ». C’est assez intuitif : c’est aussi ce qu’on a en mathématiques avec la règle « Deux quantités égales à une même troisième sont égales entre elles. ». Dans le schéma au-dessus les + indiquent qu’il s’agit d’une proposition affirmative. Dans les suivants, les – correspondront à une proposition négative.

Prenons pour exemple notre classique et perpétuel :

1. Tous les hommes sont mortels.
2. Socrate est un homme.
3. Donc Socrate est mortel.

Ici, comme la conclusion est « Donc Socrate est mortel. », on a S = Socrate et P = mortel. Les prémisses 1. et 2. sont affirmatives, donc on a bien le droit de dire que 3. (qui est aussi affirmative) est vraie.

Le syllogisme avec une conclusion négative

Cette fois, on étudie le cas où la conclusion est négative (de la forme « x n’est pas y »). On a la règle suivante : si S et P sont reliés à M de façons opposées dans les prémisses (l’un de façon positive et l’autre de façon négative), alors S et P doivent être reliés entre eux de façon négative. Encore une fois, il en existe une variante mathématique : « Deux quantités reliées de façon opposées à une troisième diffèrent entre elles. ».

Il y a deux sous-cas :

1. Soit on a S et M sont reliés dans une prémisse positive et M et P dans une prémisse négative. Alors, S et P sont reliés de façon négative dans la conclusion.

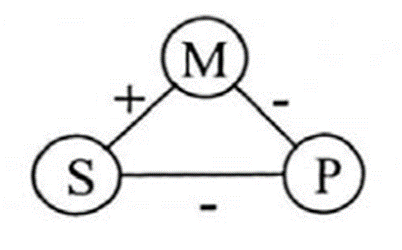
Par exemple :

Aucun mortel n’est un dieu.
Tous les hommes sont mortels.
Donc aucun homme n’est un dieu.

2. Soit on a S et M reliés dans une prémisse négative et M et P dans une prémisse positive. Alors, S et P sont reliés de façon négative dans la conclusion.

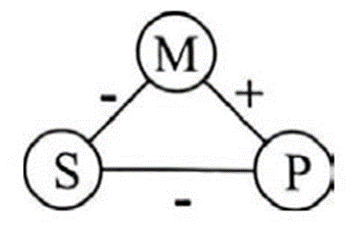
Par exemple :

Tous les ordinateurs sont des machines.
Les hommes ne sont pas des machines.
Donc aucun homme n’est un ordinateur.

Le pseudo-syllogisme où S et P sont tous deux reliés à M négativement

Dans ce cas, on ne peut rien en déduire sur la conclusion. Par exemple :

Aucun homme n’est un insecte.
Aucun insecte n’écrit des livres de logique.
Donc aucun homme n’écrit des livres de logique.

On voit bien que des deux prémisses, on ne peut pas en tirer cette conclusion.

Pour une étude beaucoup plus complète des syllogismes (qui fait plus de cent pages !), lire le livre de Maritain : Jacques Maritain, Éléments de philosophie (t. 2. L’ordre des concepts. 1.- Petite logique. 2.- Grande logique), Paris : Pierre Téqui, 1987, pp. 239-342.

Illustration : Charles Laplante, Éducation d’Alexandre par Aristote, gravure, 1866.

1. Le lecteur pensera probablement que cela fait en tout beaucoup de terminologies à maîtriser. Mais cela est nécessaire pour évaluer correctement les arguments qui se réduisent souvent à des syllogismes.[↩]