Cet article est le dixième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Le neuvième présentait de manière accessible le problème des universaux : l’un des problèmes les plus anciens et les plus difficiles de la philosophie. Cet article explique deux notions : ce que sont l’extension et la compréhension des termes. Comme d’habitude, je reprendrai énormément le contenu du livre de Peter Kreeft, Socratic Logic des pages 43 à 46.
L’extension et la compréhension d’un terme sont deux manières de le définir. Si vous avez fait des mathématiques, vous avez peut être déjà rencontré ces deux notions. Ce qui est normal comme la logique classique et la logique formelle/mathématique ont des points communs.
I. L’extension d’un terme
L’extension d’un terme est l’ensemble des choses auxquelles ce terme peut se référer. En gros, c’est la “population” de ce terme. Avec l’extension, on définit une terme de manière quantitative (en fonction des individus qu’il contient). Pour une définition plus technique :
L’extension de l’idée est l’ensemble des individus auxquels l’idée est attribuable. Tous les prêtres, passés, présents, à venir ou simplement possibles, sont contenus sous l’extension de l’idée d’homme.
ROBERT, Arthur, Leçons de logique, Québec : Action Sociale limitée, 1915, [1ère éd. 1914], p. 12.
Par exemple, l’extension du terme homme au sens large (ou man en anglais ou 人 rén en chinois) est l’ensemble de l’humanité (les six milliards d’êtres humains sur terre) qui inclut moi, vous, vos parents, vos amis, vos collègues, les miens, etc. Au sens étroit du terme (les “garçons”), l’extension du terme homme, c’est l’ensemble de tous les garçons de la planète (moi, Maxime, mon père, le sien, etc.).
Pour prendre un exemple mathématique, si je veux définir l’ensemble des nombres pairs avec l’extension, je dirais que c’est l’ensemble qui contient 0, 2, 4, 6, 8, 10, etc. Plus formellement {0, 2, 4, 6, 8, 10, …}.
II. La compréhension d’un terme
La compréhension d’un terme est ce qu’il signifie, sa définition précise avec des qualités qu’il inclut (comprend). “Compréhension” ne veut pas dire ici comprendre une idée (“D’accord, j’ai compris !”) mais inclure (“La catégorie des chiens inclut les chihuahuas et les pitbulls.”) une ou plusieurs choses. Avec la compréhension, on définit un terme de manière qualitative (en fonction de ses qualités) avec des propriétés. On analyse la compréhension d’un terme grâce à des définitions logiques.
La compréhension ou le contenu de l’idée est l’ensemble des éléments que comprend ou que contient une idée. L’idée de pape contient deux éléments : chef et Église. Le pape est le chef de l’Église.
Ibid.
Par exemple, la compréhension du terme homme (man, 人 rén, etc.) est “animal rationnel”. L’être humain est un être vivant capable de sentir (de détecter des choses physiques avec ses cinq sens) et de réfléchir (d’utiliser sa raison).
Pour prendre un exemple mathématique, si je veux définir l’ensemble des nombres pairs avec la compréhension, je dirais que c’est l’ensemble qui contient des entiers naturels de la forme 2 x n où n est un entier naturel. Plus formellement {2 x n ; n ∈ ℕ}. On a bien une définition par compréhension car on a défini les nombres pairs à l’aide d’une certaine caractéristique : 2 x n.
III. Des synonymes
L’extension et la compréhension ont de nombreux synonymes qu’on utilise plus souvent (notamment en logique formelle ou mathématique).
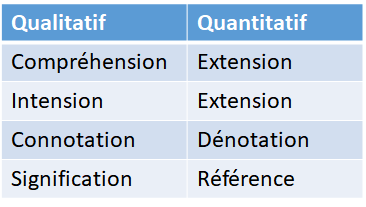
IV. Le principe de relation inverse entre extension et compréhension
Il y a une règle1 qui relie l’extension et la compréhension : les deux varient de façon inversement proportionnelle. Cela veut tout simplement dire que quand l’un des deux augmente, l’autre diminue ou que quand l’un diminue, l’autre augmente.
Prenons par exemple le terme animal. Si l’on augmente sa compréhension (sa “précision”), on obtiendra homme et on aura donc une définition plus précise qu’avant. Mais cette définition sera plus restrictive, elle inclura moins d’individus qu’avant : l’extension aura donc diminué. Cela est intuitif : il y a beaucoup moins d’individus hommes (il y a seulement tous les hommes) que d’individus animaux (il y a à la fois tous les hommes, tous les chats, tous les chiens, etc.). De même inversement : plus un groupe contient d’individus (une grande extension), puis il faudra une définition précise (une compréhension importante).
On peut voir la compréhension comme un filtre. Tout le monde sait que plus un filtre est précis, moins il laisse passer de choses. Exactement de la même façon, plus une définition (le filtre) est précise, moins elle laissera passer d’individus (de choses). Le filtre animal laisse passer plus d’individus que le filtre homme comme le premier est plus général que le deuxième.
Pour revenir aux maths, on voit bien que la définition des entiers naturels ℕ (qui peuvent seulement être positifs) est plus précise (et donc plus restrictive) que celle des entiers relatifs ℤ (qui peuvent être soit positifs, soit négatifs). Par conséquent, il y a moins d’entiers naturels que d’entiers relatifs. On a bien le fait que la compréhension a augmenté alors que l’extension a diminué.
V. Attention aux erreurs !
Dans la vie de tous les jours, nous faisons beaucoup d’erreurs parce que nous confondons extension et compréhension. Quand quelqu’un parle de quelque chose en utilisant la compréhension, nous croyons à tort qu’il utilise l’extension, et inversement.
A. Prendre une compréhension pour une extension
La première erreur : c’est croire que quelqu’un parle d’extension quand il parle en fait de compréhension. Par exemple, imaginons que je dise : “Les hommes sont plus grands (en taille) que les femmes”, ou : “Les poissons nagent alors que les oiseaux volent.” Je parle alors du point de vue de la compréhension (la définition avec de qualités : je compare deux choses selon leurs qualités) et non pas de celui de l’extension (comparaison d’individus précis).
Cela ne signifie pas qu’il n’y ait aucune femme qui soit plus grande qu’un homme mais qu’en moyenne, les hommes sont plus grands que les femmes. Cela ne veut pas non plus dire qu’il n’existe aucun animal qui sache à la fois nager et voler, mais que souvent, on n’en rencontre pas beaucoup.
Cette erreur, en gros, c’est refuser à tort de faire des généralisations à cause de quelques contre-exemples. Par exemple, on pourrait prétendre que l’affirmation : “Les hommes sont plus agressifs que les femmes” est fausse car “Madame X est plus agressive que Monsieur Y.” Le problème, c’est que l’affirmation de base se situe à un niveau plus abstrait (plus général) que la seconde. Elle peut être vraie même si la deuxième l’est.
B. Prendre une extension pour une compréhension
Le deuxième danger, c’est de prendre une extension pour une compréhension. Par exemple, si un ami me dit : “Tous mes livres sont des mangas”, ce serait une erreur de croire que tous les livres du monde sont des mangas. Qu’il n’y ait que des mangas et aucun autre type de livre (bandes-dessinées, romans, poésies, science-fiction, fantasy, etc.).
Cet ami me dit tout simplement que tous les livres chez lui et qu’il possède sont des mangas (affirmation du point de vue de l’extension). Il n’affirme rien du tout sur les livres en général (affirmation du point de vue de la compréhension).
Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants illustres – Savants de l’antiquité (tome 1), Paris, 1866, pp. 134-135.
- Elle marche pour la plupart des cas, bien qu’il y ait quelques exceptions.[↩]





0 commentaires
Trackbacks/Pingbacks