Cet article est le quarante-deuxième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le quarante-et-unième, j’ai présenté la distinction entre inférences immédiates et inférences médiate. Dans cet article, j’expliquerai un premier type d’inférences immédiates : les conversions (en vidéo ici). Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft des pages 167 à 170.

Définition

Un premier type d’inférences immédiates est la conversion. La conversion consiste à inverser le sujet et le prédicat dans une proposition. Par exemple :

1. « Certains enfants sont des moqueurs » deviendrait « Certains moqueurs sont des enfants. ».
2. « Tous les chiens sont des animaux » deviendrait « Tous les animaux sont des chiens. ».

Comme on peut le voir avec ces exemples, une conversion peut selon les cas être valide (conclusion qui suit la prémisse) ou invalide (conclusion qui ne suit pas la prémisse).

Comment savoir si une conversion est valide ?

Comment savoir dans quels cas la conversion est valide (conduit à une vraie proposition) ? Pour le savoir, il faut déterminer à quel type appartient la proposition qu’on cherche à convertir. Puis on saura en quel type de proposition il faudra la transformer pour que la conversion soit correcte. Mais est-il vraiment possible de lister tous les cas possibles ? Ne serait-ce pas trop long à faire ?

Aucun problème à ce niveau-là. Rappelons-nous que nous avons prévu avant d’utiliser ici et dans la suite de la série seulement quatre types de propositions. Lesquelles sont : les propositions catégoriques (A, E, I, O) dans leur forme logique¹. Il n’y aura donc que quatre différents cas à examiner.

Les règles de la conversion pour les quatre propositions catégoriques

Les cas de E et I (cas simples) : « Aucun S n’est P. » (E) et « Certains S sont P. » (I)

Les cas de E et I sont les plus simples comme on peut se contenter d’inverser la place du sujet avec celle du prédicat et obtenir directement une proposition vraie. Formellement, la conversion valide d’une proposition E donnera une nouvelle proposition E ou O. De même, la conversion valide d’une proposition I donnera une nouvelle proposition I. Trois règles qu’on peut résumer ainsi :

E => E
E => O
I => I

Par exemple :

1. La conversion valide de la proposition E « Aucun chien n’est un chat » est la proposition E « Aucun chat n’est un chien » ou la proposition O « Certains chats ne sont pas des chiens ».
2. La conversion valide de la proposition I « Certains animaux sont des chiens » est la proposition I « Certains chiens sont des animaux²».

Pourquoi ces deux règles sont-elles valides ? Parce que dans les propositions E et I le sujet et le prédicat sont distribués de la même manière. Dans la E ils sont tous deux distribués (universels), dans la I tous deux non distribués (particuliers).

On verra que les prochains cas A et O sont plus compliqués comme on a besoin de changer les quantificateurs.

Le cas de A (cas difficile) : « Tous les S sont P. »

La conversion valide d’une proposition A donne une nouvelle proposition I : A => I.

Par exemple : la conversion valide de la proposition A « Tous les chiens sont des animaux » est la proposition I « Certains animaux sont des chiens ».

Pourquoi cette règle est-elle valide ? Si l’on s’intéresse d’abord à la A, convertir une A en A contreviendrait à la règle « Un terme non distribué (particulier) ne peut être distribué (universel) dans la conclusion³». En effet, dans A, le prédicat est non distribué (particulier) alors que le sujet est distribué (universel). Inverser les deux reviendrait à rendre le prédicat distribué (universel), ce qu’il n’est pas car il est et il restera toujours non distribué (particulier).

En gros, une conversion de A à A est invalide car elle implique à tort de passer de « Tout S (distribué) est P (non distribué). » à « Tout P (distribué) est S (non distribué). ». Par exemple, passer de « Tous les Chinois sont des mangeurs de riz » à « Tous les mangeurs de riz sont chinois⁴ » est invalide.

Le cas de O (cas difficile) : « Certains S ne sont pas P. »

De même qu’avec A, la conversion d’une proposition O pour être correcte ne peut pas donner une autre proposition O. Par exemple, partir de « Certains animaux sont des chiens » pour prétendre que « Certains chiens ne sont pas des animaux » est invalide.

Pour la même raison qu’avec A, poser O => O contredirait la règle du maintien de la distributivité (universel ou particulier) des termes. Règle qui établit qu’un terme distribué (respectivement non distribué) dans une prémisse doit rester distribué (respectivement non distribué) dans la conclusion. Or dans notre cas précis, on transforme à tort un terme non distribué⁵ (le sujet de la prémisse) en un terme distribué (le prédicat de la conclusion).

Pour mieux comprendre pourquoi il y a erreur, on peut jeter un coup d’œil aux schémas suivants. Le premier ci-dessous illustre les propositions O :

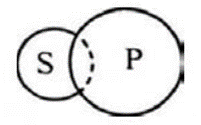
On se rappelle comme vu précédemment qu’il y a une incertitude. Les pointillés montrent qu’on sait que le sujet exclut une partie du prédicat, sans connaître pour autant la « taille » de cette partie.

Le schéma suivant représente tous les cas possibles (même si on ne sait pas lequel est le vrai) pour la proposition O « Certains S ne sont pas P » :

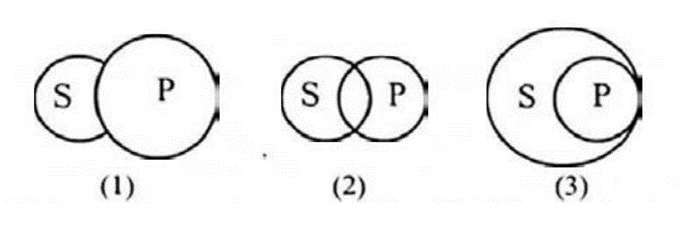
1. Soit le sujet S est complètement coupé, séparé du prédicat P ;
2. Soit le sujet se rencontre partiellement le prédicat ;
3. Soit le prédicat est entièrement inclus dans le sujet.

On voit que si le troisième cas 3) est vrai, alors la conversion O => O devient fausse. Conversion qui dit qu’à partir de la proposition « certains S ne sont pas P » (la prémisse), on sait que « certains P ne sont pas S » (la conclusion).

Justification : en effet, on observe bien que dans le schéma (3), P est dans S. Cela signifie que tous les P sont S, c’est-à-dire des « cas particuliers » de S qui partagent tous S. Par conséquent, on a bien que « tous les P sont S », ce qui contredit la conclusion « certains P ne sont pas S ». Au final, la prémisse O ne conduit pas nécessairement à une conclusion O (si on est dans le cas 3) : la conversion O => O est donc bien invalide.

Ce qu’il faut retenir : il n’y a pas de conversion valide pour les propositions O « Certains S ne sont pas P. ».

Résumé des règles de conversion

Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants illustres – Savants de l’antiquité (tome 1), Paris, 1866, pages 134-135.

1. Pour rappel, la forme logique des propositions catégoriques exige que 1) le verbe soit le verbe être et que 2) les termes (sujet et prédicat) soient des noms communs.[↩]
2. Cette proposition reste vraie même si on sait tous qu’on pourrait aller plus loin en affirmant que « Tous les chiens sont des animaux. ».[↩]
3. Si j’ai des informations sur seulement une partie d’un groupe, je n’ai pas le droit d’en déduire des informations sur le groupe entier. Par contre cela vaut uniquement pour les déductions/raisonnements déductifs que nous étudions pour le moment (contrairement aux inductions/raisonnements inductifs.[↩]
4. Les Français, les Indiens, les Africains, etc. mangent aussi du riz.[↩]
5. Car on est dans le cas d’une proposition universelle négative où le sujet est forcément non distribué.[↩]