Cet article est le quatrième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Le troisième résumait tout ce qu’il y a d’important à retenir sur la logique. Cet article développe plus en détails le précédent sur les trois opérations de l’intelligence (appréhension, jugement et raisonnement). Comme d’habitude, je reprendrai énormément le contenu du livre de Peter Kreeft, Socratic Logic des pages 28 à 33.

I. Les trois opérations de l’intelligence

La logique repose sur deux faits évidents : les êtres-humains pensent et leur pensée a une structure (elle n’est pas « en bazar », mais ordonnée). On peut étudier cette pensée humaine à partir de différents points de vue.

Par exemple, le neurologue va chercher à découvrir ce qui se passe dans le cerveau d’une personne en train de réfléchir (quelle zone s’active, etc.) La politique étudie la différence entre les « pensées des capitalistes » et les « pensées des communistes ». En logique, il y a trois types de pensées qu’on appelle les trois opérations¹ (dans le sens d’une action) de l’intelligence :

1. L’appréhension simple ;
2. Le jugement ;
3. Le raisonnement.

1) L’appréhension simple² correspond à ce que l’on fait quand on conçoit, comprend ou saisit un concept exprimé par un terme ou un mot, une chose à laquelle on pense comme un « homme », « un chien » ou un « chien malade ». C’est la première opération de l’intelligence.

La simple appréhension est l’acte par lequel l’intelligence perçoit l’essence d’une chose sans affirmer et sans nier quoi que ce soit de cette essence.

ROBERT, Arthur, Leçons de logique, Québec : Action Sociale limitée, 1915, [1ère éd. 1914], p. 11.

On a vu comment l’intelligence appréhendait une chose et s’en formait un concept par abstraction. Cette appréhension simple est la première étape : la saisie de la quiddité, le “ce que c’est” de la chose, son objet propre et premier. Elle appréhende homme, par exemple, c’est-à-dire qu’elle saisit “ce qu’est” l’homme et le conçoit comme un certain être qu’elle va alors distinguer des autres : un être animé, doué de la sensibilité et raisonnable.

COUILLAUD, Bruno, Raisonner en vérité, Paris ; Perpignan : Desclée de Brouwer, 2014, [1ère éd. 2003], p. 55.

2) Le jugement³, c’est ce que l’on fait tous quand on connecte deux mots (le sujet et le prédicat), plus précisément quand on dit quelque chose (le prédicat) à propos de quelque chose d’autre (le sujet).

Cette connexion d’un sujet et d’un prédicat, on l’appelle une proposition⁴. Le sujet est toujours quelque chose d’individuel/concret alors que le prédicat est une qualité universelle qui peut être partagée par plusieurs choses (sujets) contrairement au sujet. Pour ne pas les confondre, on peut retenir que le jugement est une action (de l’intelligence) et la proposition le résultat du jugement.

Par exemple, en disant « Laurent est chinois », je relie « Laurent » (le sujet) à « chinois » (le prédicat). La qualité “chinois” est partagée par tous les chinois du monde. Par contre Laurent ne peut pas être partagé : Laurent, c’est moi, et personne d’autre. On voit que le jugement est plus complexe que l’appréhension simple. C’est en quelque sorte « la suite » de l’appréhension. Cette seconde opération de l’intelligence se construit sur la première.

Pour finir, on peut noter que le jugement permet d’aller plus que loin que l’appréhension simple. En effet, l’appréhension simple permet de saisir les essences des choses mais est incapable de se prononcer sur leur existence. Concrètement, elle nous permet de savoir ce que sont (leurs essences) les choses (un chien, un chat, une licorne, Superman, les dinosaures). Mais elle est incapable de nous dire si elles existent ou pas (leur existence). Alors que le jugement nous permet de savoir si les choses existent ou non.

Le jugement est un acte par lequel l’esprit affirme ou nie qu’une chose est. Ex. : Dieu est bon. L’homme n’est pas impeccable.

ROBERT, Leçons de logique, op. cit., p. 29.

Mais l’intelligence rejoint aussi les propriétés qui se rapportent à l’être qu’elle a saisi antérieurement ; l’homme, comme être fait pour vivre en société, ou comme doué de langage par exemple : elle va alors composer ses concepts pour affirmer l’existence de ce qu’exprime l’un dans les sujets auxquels renvoie l’autre : tout homme est social.

COUILLAUD, Bruno, Raisonner en vérité, op. cit., p. 55.

3) Le raisonnement, c’est relier non plus juste des mots, mais plusieurs propositions : plusieurs qu’on regroupe dans les prémisses et une autre qui est la conclusion. Cette connexion de propositions ne se fait pas au hasard, mais dans un ordre : la conclusion est la conséquence logique des prémisses. D’abord les prémisses, puis la conclusion. Comme avant avec le jugement et la proposition, on distingue entre le raisonnement qui est l’action (de l’intelligence) et l’argument⁵.

Si les prémisses sont vraies, alors la conclusion est vraie. Le raisonnement est la troisième opération de l’intelligence : la suite du jugement. Une nouvelle fois, on voit que le raisonnement (troisième opération) est plus complexe que le jugement (deuxième opération).

Le raisonnement est la troisième opération de l’esprit humain. Il est l’acte par lequel un jugement est déduit légitimement de deux autres. Ou encore, il est l’acte par lequel l’esprit humain d’une vérité connue infère une vérité inconnue. […] Le raisonnement se définit encore comme suit : c’est une opération par laquelle l’esprit humain d’une connaissance donnée déduit une connaissance nouvelle.

ROBERT, Leçons de logique, op. cit., p. 35.

II. Les trois produits des trois opérations de l’intelligence

Ces trois opérations de l’intelligence produisent trois types d’objets différents auxquels nous pensons tous les jours. Appelons-les à partir de maintenant « produits de l’intelligence » car ce sont des idées abstraites que notre intelligence produit lorsque nous réfléchissons ou pensons à quelque chose :

1. Les concepts (le résultat de l’acte de concevoir) ;
2. Les jugements (le résultat de l’acte de juger) ;
3. Les arguments (le résultat de nos raisonnements, de nos argumentations).

On peut s’intéresser à chacun de ces produits soit sous le point de vue de la logique, soit sous celui du langage (la discipline qui étudie les langues : le chinois, le français, l’arabe, l’anglais, etc.) Ils ont alors un nom différent. En logique, on parle :

1. De termes ;
2. De propositions ;
3. D’arguments.

Alors qu’en linguistique, on parle :

1. De mots ou d’expressions (moins complètes qu’une phrase) ;
2. De phrases déclaratives ;
3. De paragraphes ou la connexion d’au moins deux phrases déclaratives par un mot de liaison comme « donc » qui indique qu’on a là un argument.

Voici des exemples :

1. « Homme » ;
2. « Socrate est un homme » ;
3. « Tous les hommes sont mortels, or Socrate est un homme, donc Socrate est mortel. »

III. Les différences entre la logique et le langage

On peut remarquer plusieurs différences entre la logique et le langage :

1. La logique ne se préoccupe que d’une seul type de phrases : les phrases déclaratives qu’elle appelle propositions, autrement dit les phrases où quelqu’un affirme quelque chose, donne son avis. Au contraire, le langage prend en compte plusieurs types de phrases : non seulement les phrases déclaratives (« J’ai rencontré votre chien dans la rue aujourd’hui. ») mais aussi les phrases interrogatives (« Comment s’appelle votre chien ? »), les phrases impératives (« Debout, couché mon chien ! ») et les phrases exclamatives (« Votre chien est gros ! »).
2. La logique est naturelle (dans le sens de non inventée par l’homme), alors que le langage (plus généralement toutes les langues) est artificiel.
3. Il existe plusieurs langues qui varient en fonction du lieu et du temps alors qu’il n’y a qu’une seule et unique logique qui est partout et tout le temps la même dans le monde entier. Il n’y a pas une logique « chinoise » différente d’une logique « française ». La logique est aussi universelle et objective que les mathématiques. Par contre, elle prend différentes formes (différentes langues) dans différents pays.

IV. La structure des trois produits de l’intelligence

Nous allons maintenant étudier la composition des trois produits de l’intelligence. De quoi est-ce qu’ils sont composés ?

1. Un terme ne peut pas être divisé en plusieurs parties, il est indivisible. Il n’y a pas d’unité, de « brique » plus fondamentale ou basique. Un peu de la même manière qu’il n’y a rien de plus petit que les atomes (maintenant les quarks) en chimie ou que le nombre un en mathématiques. Par exemple, « Socrate » et « mortel » sont des termes.
2. Une proposition est composée de deux termes : un terme appelé le sujet et un autre prédicat. On retrouve les mêmes définitions qu’en grammaire : le sujet est ce de quoi on parle et le prédicat est ce qu’on dit sur le sujet. Dans la proposition « Socrate est mortel », « Socrate» est le sujet et « mortel » est le prédicat.
3. Un argument est composé de deux groupes de propositions : les prémisses et la conclusion. Les prémisses sont les propositions que l’on suppose (en fait qu’on doit montrer) vraies et qui servent à justifier la conclusion. La conclusion est ce qu’on cherche à prouver, le résultat final de l’argument. Dans l’exemple précédent « Tous les hommes sont mortels, or Socrate est un homme, donc Socrate est mortel. », on a deux prémisses : « Tous les hommes sont mortels. » et « Or Socrate est un homme. » et la conclusion : « Donc Socrate est mortel. ».

En résumé :
1. Composantes d’un terme : aucune ;
2. Composantes d’une proposition : un sujet (un terme) et un prédicat (un autre terme) ;
3. Composantes d’un argument : les prémisses (plusieurs propositions) et une conclusion (une proposition).

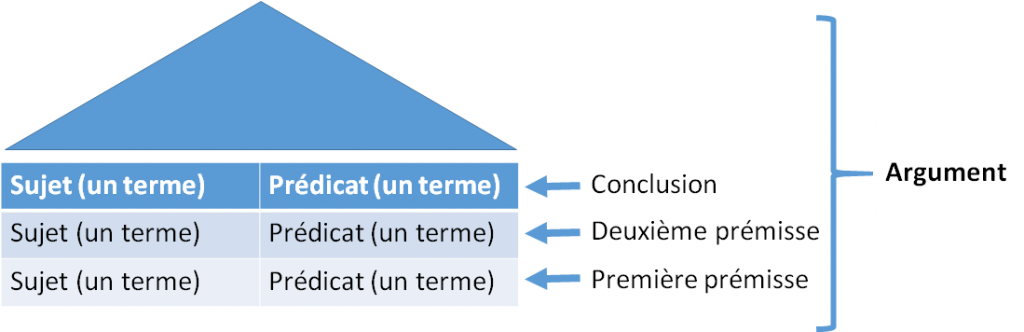
Pour être sûr de bien comprendre comment toutes ces choses sont liées, on peut penser à une maison avec trois étages (on va prendre un type d’argument qui s’appelle le syllogisme) auxquelles se trouvent plusieurs pièces.

1. La maison : c’est l’argument.
2. Les trois étages : ce sont les propositions, les deux premiers sont les prémisses et le dernier la conclusion.
3. Les pièces de chaque étage : ce sont les termes de chaque proposition

On voit que de même que la maison dépend de ses parties (les étages), un argument dépend aussi des siennes (les propositions). Encore pareil si l’on pense aux étages : de la même façon qu’ils dépendent de leurs pièces, les propositions dépendent de leurs termes. Le dernier étage dépend des deux dessous : s’ils s’écroulent, lui aussi. Encore la même chose : sans les prémisses, la conclusion s’écroule.

V. Les trois questions auxquelles les produits de l’intelligence répondent

Chacune de ces entités logiques (termes, jugements et raisonnements) répondent à trois questions différentes :
1. Un terme répond à la question « Qu’est-ce que c’est ? »
2. Une proposition répond à la question : « Est-ce bien le cas ? »
3. Un argument répond à la question : « Pourquoi ? »

Par exemple :
1. Un enfant pointe du doigt un castor et demande « Qu’est-ce que c’est ? » : « Un castor »
2. « Est-ce que ce castor est intelligent ? » : « Le castor est intelligent. »
3. « Pourquoi est-il intelligent ? » : « Parce que tous les castors sont intelligents, or cet animal est bien un castor, donc il est aussi intelligent. »

VI. Les trois aspects de la réalité révélés

Chacune des entités logiques nous révèlent un aspect particulier de la réalité :
1. Les termes révèlent les essences (ce que cette chose est) ;
2. Les propositions révèlent l’existence (est-ce que cette chose existe) ;
3. Les arguments révèlent les causes (pourquoi cette chose est comme ça).

VII. La mise en pratique de la logique

Nous avons fini de voir les bases théoriques de la logique. En pratique, quand on fait de la logique, le but est de faire la différence entre des termes clairs et des termes ambigus, des propositions vraies et des propositions fausses, et des arguments logiquement valides et des arguments logiquement invalides. En résumé :
1. Les termes sont soit clairs soit ambigus ;
2. Les propositions sont soit vraies soit fausses ;
3. Les arguments sont soit valides soit invalides.

Je pense que « clair », « ambigu », « vrai » et « faux » sont évidents. Un argument est « valide » quand sa conclusion suit nécessairement ses prémisses. Par exemple, cet argument est valide :
Tous les hommes sont mortels.
Or je suis un homme.
Donc je suis mortel.

Mais pas celui-ci :
Tous les hommes sont mortels.
Or tous les cochons sont mortels.
Donc tous les cochons sont des hommes.

Ni celui-ci, même si sa conclusion et ses prémisses sont vraies :
Tous les hommes sont mortels.
Or Socrate est mortel.
Donc Socrate est un homme.

Il faut remarquer que la logique n’est pas seulement une discipline théorique, mais qu’elle est aussi pratique. Pratique parce qu’elle ne nous dit pas seulement ce que ou comment les choses sont, mais ce qu’elles devraient être. La logique nous dit ce qu’un bon argument doit être. Ainsi, la logique permet d’améliorer nos arguments, elle est comme un juge qui les teste.

Voici un tableau qui résume les différentes possibilités⁷, vous remarquerez qu’il n’y a qu’un seul cas où la conclusion est bien prouvée :

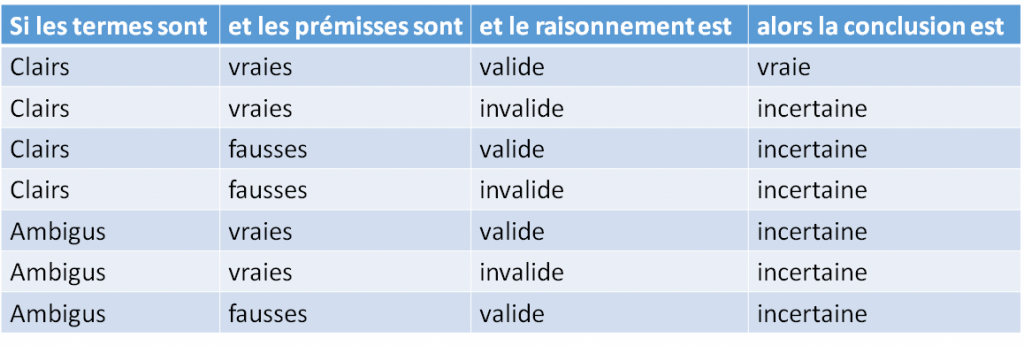
Quand je dis que la conclusion est incertaine, je veux dire qu’avec cet argument précis qui est faux, on ne peut pas savoir si la conclusion est vraie. Mais ce n’est pas forcément parce qu’un raisonnement est faux que sa conclusion est aussi fausse. Peut-être qu’il existe un autre argument correct qui permet de prouver cette conclusion. En gros, ce n’est pas parce qu’on s’est trompé de chemin une fois qu’il n’en existe pas un bon pour arriver là où on veut.

VIII. Attention à ne pas s’embrouiller !

Un danger est de confondre « clair », « vrai » et « valide ». Pour pouvoir ne pas être perdu dans la suite de la série, il est très important de comprendre que :

1. Les termes ne sont jamais vrais ou faux ; ce sont les propositions qui les contiennent qui sont vraies ou fausses.
   Les termes ne sont jamais valides ou invalides : seuls les arguments sont valides ou invalides.
   Les termes sont clairs ou ambigus.
2. Les propositions ne sont jamais claires ou ambigües ; ce sont leurs termes qui sont clairs ou ambigus.
   Les propositions ne sont jamais logiquement valides ou invalides en elles-mêmes ; ce sont les arguments qui les contiennent qui sont soit logiquement valides ou invalides.
   Les propositions sont vraies ou fausses.
3. Les arguments ne sont jamais clairs ou ambigus ; ce sont tous les termes contenus dans l’argument qui sont clairs ou ambigus.
   Les arguments ne sont jamais vrais ou faux. Chaque proposition d’un argument est vraie ou fausse.
   Les arguments sont soit valides ou invalides.

IX. Ce que la logique permet de faire

La logique nous permet de faire deux choses assez facilement : d’abord définir nos termes de sorte à ce qu’ils soient clairs et non-ambigus et ensuite savoir quand est-ce qu’un argument est valide ou invalide. Cependant, elle n’a pas de recette miracle, de méthode qui marche tout le temps efficace pour vérifier si une proposition est vraie ou fausse. Pour cela, il faut utiliser d’autres moyens : notre intuition, nos expériences scientifiques, nos observations, nos raisonnements, écouter et faire confiance à des personnes qui font autorité.

Mais que veut dire « la vérité » ? Nous le savons en fait déjà tous intuitivement mais précisément, c’est savoir ou dire d’une chose qu’elle est ce qu’elle est. Par exemple, si je dis « Ce chat est gros » et que le chat est vraiment gros, alors ce que j’ai dit est vrai. Par contre, si le chat est maigre, j’aurais dit quelque chose que le chat n’est pas (« gros »), dans ce cas j’aurais faux.

X. Comment tester nos arguments

Il faut se poser ces trois questions :
1. Que voulez-vous dire ? (Définissez vos termes.)
2. Où voulez-vous en venir ? (Quelle est votre conclusion ?)
3. Pourquoi ? (Prouvez-le.)

Et être sûr de trois choses :
1. Être sûr que vos termes sont clairs ;
2. Être sûr que vos prémisses sont vraies ;
3. Être sûr que votre raisonnement est valide.

Une fois ces conditions remplies, vous pouvez être sûr d’avoir réussi à prouver votre conclusion. Enfin, pour montrer que quelqu’un se trompe dans sa réflexion, il faut trouver au moins une de ces erreurs :
1. Un terme est ambigu.
2. Une prémisse est fausse.
3. Un raisonnement est un sophisme (c’est-à-dire un raisonnement invalide).

Si vous ne trouvez aucune erreur, vous êtes obligés d’accepter que sa conclusion est vraie.

Conclusion : un résumé

Voici un tableau qui résume toute cette section⁸ :

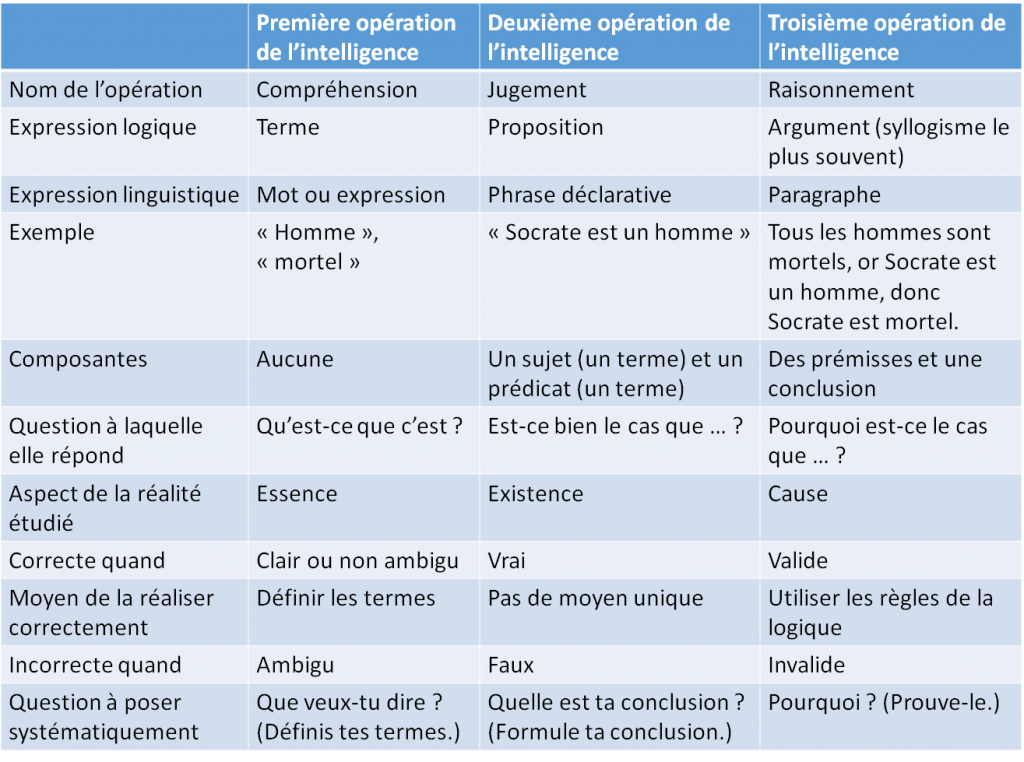
Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants illustres – Savants de l’antiquité (tome 1), Paris, 1866, pages 134-135.

1. Par opération, nous désignons un acte dont le terme est une perfection inhérente à une puissance : l’opération de la vision, par exemple, met la puissance visuelle parfaitement en acte si rien ne vient l’empêcher tant du côté de l’objet qui doit être proportionné à la puissance (on ne peut regarder le soleil en face par exemple) que du côté de la puissance et de son support organique (une déficience ou une maladie dans l’organe entrave le bon déroulement de l’opération). Référence : COUILLAUD, Bruno, Raisonner en vérité, Paris ; Perpignan : Desclée de Brouwer, 2014, [1ère éd. 2003] p. 55.[↩]
2. Aussi appelée la simple appréhension, la conception ou tout simplement l’appréhension de l’idée de la chose, de sa quiddité, par exemple dans COLLIN, Henri, Manuel de philosophie thomiste Tome II Psychologie, Paris VI : Pierre Téqui, 1949, p. 244[↩]
3. Aussi appelée composition/division (composition est synonyme d’affirmation, division de négation). Certains préfèrent conserver au jugement “son sens de terme parfait de l’opération intellectuelle : la connaissance vraie et surtout certaine. Vraie parce qu’adéquate, l’adéquation au réel étant la propriété de la deuxième opération […] certaine parce que la certitude est une détermination ferme de l’intelligence, une adhésion complète à la proposition énonçant le jugement en raison d’une argumentation. En ce sens, un jugement parfait n’est possible que par une démonstration et une résolution, c’est-à-dire cet acte de voir la conclusion dans les principes premiers.”. Référence : COUILLAUD, Bruno, Raisonner en vérité, op. cit., p. 197.[↩]
4. Aussi appelée énonciation ou discours énonciatif. Référence : COUILLAUD, Bruno, Raisonner en vérité, op. cit., p. 202, 217.[↩]
5. Ou argumentation. Référence : COUILLAUD, Bruno, Raisonner en vérité, op. cit., p. 239.[↩]
6. Ibid.[↩]
7. Socratic Logic, p. 32[↩]
8. Socratic Logic, p. 33[↩]