Cet article est le quarantième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le trente-neuvième, j’ai présenté d’autres types de propositions délicats qui prêtent à confusion. Dans cet article, j’expliquerai la distinction entre termes distribués et termes non distribués. Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft des pages 163 à 164.

Terme distribué et terme non distribué

Dans une proposition catégorique, chaque terme (le sujet et le prédicat) est soit distribué, soit non distribué :

1. On dit qu’un terme est distribué s’il est universel. C’est-à-dire si la proposition dans laquelle il se trouve prétend apporter une information sur tous les membres d’un groupe auquel ce terme fait référence.
2. Inversement, il est non distribué s’il est particulier. Si la proposition prétend apporter une information seulement sur certains membres de ce groupe.

Buts de cette distinction distribué/non distribué

Comme nous le verrons plus tard dans la série, celle-ci nous permet de tester facilement si un argument est valide ou non. Elle nous fait aussi remarquer que les propositions E sont celles qui ont les plus grandes prétentions en termes de connaissances et les I les plus petites. En effet, dans les E, tous les termes sont distribués tandis que dans les I, ils sont tous non distribués.

Comment savoir si le sujet est distribué ou non distribué ?

Le cas du sujet est facile et assez intuitif une fois qu’on a les propositions dans leur forme logique :

1. Dans le cas d’une proposition universelle (A ou E), le sujet est distribué. Par exemple, on voit bien que lorsqu’on affirme que « tous les hommes sont mortels », on parle bien d’une caractéristique qui concerne tous les hommes.
2. Dans le cas d’une proposition particulière (I ou O), le sujet est non distribué. Par exemple, il est évident qu’on dit quelque chose uniquement à propos de certains hommes quand on affirme que « quelques hommes sont des héros. ».

Comment savoir si le prédicat est distribué ou non distribué ?

Le cas du prédicat est plus compliqué.

1. Le prédicat d’une proposition affirmative est non distribué.
2. Le prédicat d’une proposition négative est distribué.

1. Les diagrammes d’Euler pour A et E confirment la première règle

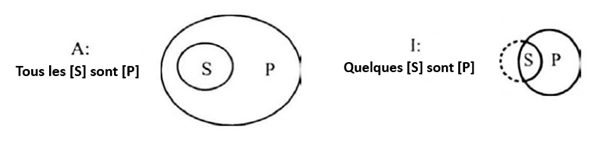
Dans le cas des propositions affirmatives, on voit qu’on n’a toujours qu’une information partielle sur le prédicat (le cercle P). En effet, à chaque fois, que le cercle S soit inclus dans le cercle P complètement (A) ou partiellement (E), il ne recouvre jamais tous le cercle P mais seulement une partie.

2. Les diagrammes d’Euler pour E et O confirment la deuxième règle

Dans le cas des propositions négatives, on voit qu’on a toujours une information « globale » sur le prédicat (le cercle P). On voit que tout le cercle P est exclu d’au moins une partie du cercle S (le cas O) ou de tout le cercle S (le cas E). Autrement dit, on sait qu’une proposition négative exclut le sujet de tout son prédicat.

Résumé

Les universelles affirmatives ont un sujet distribué et un prédicat non distribué.
Les universelles négatives ont à la fois le sujet et le prédicat distribués.
Les particulières affirmatives ne distribuent ni le sujet ni le prédicat.
Les particulières négatives ont un sujet non distribué et un prédicat distribué.

Shahid Rahman et al., « Le syllogisme catégorique », p. 5.

On peut regrouper tous ces différents cas dans ce schéma :

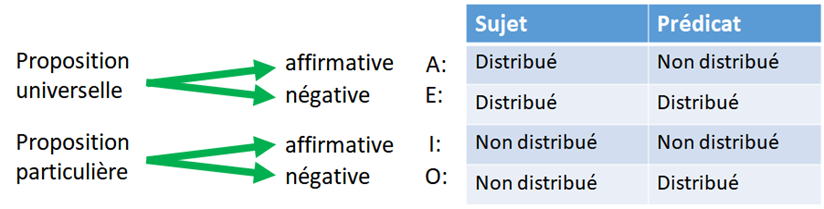
On peut encore le simplifier et le rendre plus facile à retenir avec les notations ci-dessous. Cela nous sera utile pour vérifier facilement si un syllogisme (un type d’argument) est valide.

1. Les lettres majuscules S (pour le sujet) et P (pour le prédicat).
2. Les lettres minuscules d (pour distribué) et n (pour non distribué) au-dessus du sujet (S) et du prédicat (P). C’est une notation en puissance comme en mathématiques, même s’il ne s’agit que d’une coïncidence.

A : Tous les S^d sont Pⁿ.
E : Aucun S^d n’est P^d.
I : Quelques Sⁿ sont Pⁿ.
O : Quelques S^u ne sont P^d.

Illustration : Éducation d’Alexandre par Aristote, gravure de Charles Laplante, publiée dans le livre de Louis Figuier, Vie des savants illustres – Savants de l’antiquité (tome 1), Paris, 1866, pp. 134-135.