Cet article est le soixantième d’une série consacrée à la logique classique (ou aristotélicienne, c’est-à-dire développée par Aristote). Dans le cinquante-neuvième, j’ai présenterai l’objection du sceptique au syllogisme et proposerai une réponse. Dans cet article, j’en ferai de même mais cette fois-ci avec l’objection empiriste au syllogisme. Comme d’habitude, je reprendrai énormément le contenu du livre Socratic Logic de Peter Kreeft, pp. 222-230.

---

Les objections que nous allons voir proviennent des empiristes (ex : les deux philosophes britanniques connus John Stuart Mill et David Hume) qui doutent que notre connaissance puisse porter sur autre chose que des individus particuliers. Dit autrement qui pensent que connaître les essences universelles des choses est chose impossible ou tout simplement que les universaux n’existent pas (si c’est le cas, ils sont donc nominalistes, ce qui est souvent le cas des empiristes). Nous allons examiner les deux arguments empiristes contre le syllogisme (en tout cas, ce sont ceux relevés par Kreeft).

Premier dilemme : le dilemme classique « tautologie ou non sequitur »

Résumé du dilemme     

Selon eux, les partisans du syllogisme tombent dans le dilemme suivant :

1. Soit la conclusion du syllogisme ne fait que répéter avec des mots différents ce qui a déjà été dit dans les prémisses, auquel cas on a une tautologie : on n’a rien appris de nouveau.
2. Soit la conclusion dit quelque chose de nouveau qu’il n’y avait pas dans les prémisses et alors on a un non sequitur : le syllogisme est donc invalide.

Exemple du dilemme

Pour mieux comprendre, prenons notre exemple immortel avec Socrate :

1. Tous les hommes sont mortels. 
2. Or Socrate est un homme. 
3. Donc Socrate est mortel. 

Il est évident que les partisans du syllogisme affirment que le syllogisme apporte de nouvelles informations. Pour justifier la prémisse qui dit que « tous les hommes sont mortels », l’empiriste prétend qu’on doit prouver à part par l’observation que chaque individu humain est bien mortel. Plus techniquement, la seule façon de prouver qu’elle est vraie, c’est de faire une énumération exhaustive par l’observation à l’aide de nos sens. Cela vaut pour toutes les propositions universelles du type « tout S est P » (positive) ou « tout S n’est pas P » (négative) où S est le sujet et P le prédicat. Ici dans notre cas particulier on a une proposition universelle positive où S = Socrate et P = mortel.

Cela revient nous oblige donc à vérifier en particulier que Socrate (un de ces individus dont il faut vérifier la mortalité) est bien mortel. Or, c’est exactement ce que le syllogisme cherche à démontrer. Comme on doit se servir de la conclusion pour prouver une prémisse, on en déduit qu’il y a un non sequitur.

Réponse au dilemme

Reprenons la proposition Q sur laquelle repose cette objection : la seule façon de prouver qu’une proposition universelle (de la forme « tout S est P» ou « tout S n’est pas P ») est vraie, c’est de faire une énumération exhaustive par l’observation à l’aide de nos sens.

Or elle est fausse : elle n’est pas vraie dans tous les cas. Tout dépend de la relation que le prédicat P a avec son sujet S. P peut, rappelons-le, être soit le genre, l’espèce, la différence spécifique, un propre ou un accident de S. Tous ces termes compliqués sont définis dans cet ancien article.

 On peut répartir tous ces types d’attributs en deux groupes. Du coup, P peut être :

1. Soit une caractéristique optionnelle, facultative (le mot technique est contingent), que S n’est pas obligé de posséder : un de ses accidents. Par exemple un être humain peut être blanc, jaune ou noir, un homme ou une femme, être gros, moyen ou maigre, petit, de taille moyenne ou grand, et ainsi de suite.
2. Soit une caractéristique que S possède forcément (le mot technique est nécessaire) car elle décrit ce qu’il est vraiment (dit quelque chose en lien avec son essence) : son genre, son espèce, sa différence spécifique qui décrivent directement l’essence ou un de ses propres (ou accidents propres ou encore propriétés) qui ne sont pas l’essence mais en découlent. Par exemple, un être humain doit forcément avoir un corps, une âme, etc.

I. Exemple dans le cas des caractéristiques contingentes ou accidents

Par exemple, dans ce syllogisme, P = une bande dessinée est un accident :

1. Tous les livres dans ma chambre sont des bandes dessinées.
2. Ce livre est un livre dans ma chambre.
3. Donc ce livre est une BD.

En effet il n’est pas nécessaire par principe qu’un livre soit une bande dessinée car il en existe plein d’autres sortes : des romans, des mangas, des essais, des poésies, etc. Il est « accidentel » (optionnel) pour mes livres d’être tous des bandes dessinées : j’aurais très bien pu acheter des romans à la place ou en plus. Dans ce cas, effectivement, il est impossible de savoir que 1. est vrai avant d’avoir vérifié un par un que tous les livres dans ma chambre sont tous des bandes dessinées.

II. Exemple dans le cas des caractéristiques nécessaires

Par contre, dans notre syllogisme avec Socrate les choses sont différentes. Le prédicat P n’est plus accident mais un propre, une propriété inhérente et nécessaire au sujet S. Dans ce cas, l’expérience nous montre qu’on n’a pas besoin d’énumération exhaustive par les sens.

On peut saisir un concept universel (ici le propre) par le processus d’abstraction après avoir été confronté à plusieurs exemples particuliers. Dans le cas qui nous intéresse ici, on peut savoir que la majeure du syllogisme (par ex. « tout homme est mortel ») est vraie car on parvient à comprendre les attributs/universaux d’un homme (ce que ça veut dire en général d’être humain) et de mortel après avoir vu quelques exemples et bien compris les différents types d’attributs des hommes. On sait que chaque homme est mortel car on sait par abstraction que chacun a un corps physique (et qu’un corps, par définition, peut dépérir, se décomposer, arrêter de fonctionner, mourir…) et que c’est une caractéristique nécessaire de chaque homme (tout homme la possède forcément), contrairement au fait de mesurer 1 m 20, 1 m 80 ou une autre taille, d’être blanc, noir ou jaune, d’avoir une voix grave ou aigüe et ainsi de suite pour toutes les autres caractéristiques secondaires. Tout le monde sait que tous ces attributs varient et qu’aucun n’est crucial pour définir ce qu’est un homme. Autrement dit, on est capable de faire la différence entre les propres et les accidents d’un homme, et de même pour beaucoup d’autres choses en général.

C’est exactement de cette manière qu’un enfant de trois ans arrive à reconnaître un chat — même ceux qui ont des différences avec tous ceux qu’elle a vus avant. Même s’il n’a vu que des petits chats tout blancs, quand il verra un gros chat noir, il saura que c’est un chat. Car il aura compris que ce n’est pas la taille (à plusieurs centimètres près), ni la couleur qui fait le chat mais des attributs plus généraux comme la moustache, avoir des griffes, miauler, avoir des oreilles en forme de triangle, etc.

Pour conclure, il est pertinent de dire que les universaux existent et qu’on peut les connaître par la compréhension (la première opération de l’esprit), car cette théorie a un fort pouvoir explicatif.

Le philosophe thomiste Henri Collin écrit la même chose avec des mots plus techniques :

On objecte la règle générale que la conclusion ne doit pas dépasser les prémisses ; or cette règle est violée dans l’induction, puisqu’on aboutit à une conclusion universelle, à partir de cas particuliers. Cette objection n’a de valeur que contre la conception empiriste de l’induction, qui reste dans le domaine sensible et étend à tous les cas une propriété vérifiée seulement en quelques-uns. En réalité, l’induction atteint un type d’être universel (le métal) et non une collection d’individus (tous les métaux !). Or ce type d’être universel est vraiment aperçu par l’esprit en chacun des corps concrets en même temps que la propriété commune qu’ils possèdent. Dès que l’expérience, suffisamment poussée, révèle entre ce type d’être et la propriété en question (la conductibilité) un rapport constant et exclusif, la raison est autorisée à l’affirmer. La constance de ce rapport n’est pas déduite des cas particuliers, elle est constatée, lue en eux, et abstraite de leurs caractères individuants, comme l’intelligible est dégagé du sensible. Mais ici l’intelligible est un rapport, au lieu d’être une simple essence.

COLLIN, Henri, Manuel de philosophie thomiste Tome I Logique formelle – Ontologie – Esthétique, Paris VI : Pierre Téqui, 1949, p. 75.

Pourquoi les empiristes mélangent accidents et les autres caractéristiques liées à l’essence ?

Pour comprendre pourquoi ils mélangent accidents et les autres caractéristiques liées à l’essence, il faut comprendre que les accidents sont des caractéristiques particulières tandis que les autres sont universelles.

• Les accidents sont particuliers car ils décrivent des qualités que des individus d’un même type ne sont pas obligés de tous posséder : elles ne décrivent donc pas l’essence de ce type.
• Les autres sont universels car ils décrivent des qualités que tous les individus d’un même type ont forcément en commun : toutes ces qualités décrivent l’essence de ce type, c’est-à-dire ce qu’il est profondément.

Les empiristes (et c’est la thèse pour laquelle ils tiennent leur nom) pensent que la seule méthode fiable pour acquérir de la connaissance est l’expérience par les sens (toucher, regarder, manger, entendre, etc.) des choses particulières (le chien de ma voisine, le chien de mon ami, le chat errant dans un lac, la cerise que j’ai mangée hier midi, etc.) et que nous ne pouvons pas aller plus loin que le particulier pour rejoindre l’universel. C’est pourquoi soit ils rejettent l’existence des essences universelles (c’est le nominalisme) et relèguent au rang des accidents sensibles, soit tout en reconnaissant leur existence, ils jugent qu’il est impossible d’y accéder¹. Mais c’est faux : on peut aussi connaître en comprenant des universaux (par abstraction des essences universelles). Relire la partie Exemple dans le cas des caractéristiques nécessaires ci-dessus si besoin.

Deuxième dilemme : issu de la logique formelle

Pour dire que S est P à l’aide du syllogisme, on tombe à nouveau dans un dilemme : 

1. Soit on dit que S et P sont la même chose (S = P) et donc le syllogisme (en particulier sa conclusion) n’apporte aucune information : le prédicat ne fait que répéter le sujet sous une autre forme. Par conséquent, il est inutile. 
2. Soit on dit que S et P ne sont pas la même chose et alors on tombe à nouveau dans le non sequitur : comme S et P sont (sous-entendu complètement) différents, on n’a pas le droit de dire dans la conclusion que S est P. Sinon on violerait le principe d’identité (expliqué en détails ici). 

Ce dilemme est faux car il omet une troisième possibilité qui est la suivante. S n’est ni identique à P, ni complètement différent de P, S est un aspect du sens de S (un prédicable) qui peut être :

1. Son genre : son aspect (de son essence) qu’il a en commun avec d’autres choses ;
2. Sa différence spécifique : son aspect (de son essence) qui le distingue des autres membres de son genre ;
3. Son espèce : l’essence prise dans son entièreté, genre + différence spécifique ;
4. Un de ses propres : un aspect qui découle nécessairement et toujours de son essence sans être son essence elle-même ;
5. Son accident : ni un aspect de son essence, ni quelque chose qui en découle nécessairement et toujours, donc quelque chose qui est parfois présent, parfois non (toutes ces notions expliquées en détail ici).

L’induction, vraiment supérieure à la déduction ?

À l’époque, Stuart Mill avait justement proposé son dilemme pour prouver que l’induction est supérieure à la déduction. C’est souvent le cas aujourd’hui où en général, les empiristes (comme John Stuart Mill) privilégient de loin l’utilisation de l’induction (principalement à travers la formulation de théories scientifiques mais nous y reviendrons dans la partie d’après) et méprisent la déduction qu’ils relèguent aux côtés des vieilles philosophies périmées inutiles.

En réalité, le dilemme « tautologie ou non sequitur » de Stuart Mill contre la déduction est également fatal à l’induction :

1. Soit les prémisses traitent déjà de tous les cas (on a une induction complète) dont parle la conclusion : auquel cas l’induction n’est qu’une tautologie.
2. Soit elles ne traitent pas de tous les cas : on a alors un non sequitur.

Par conséquent, les arguments inductifs suivants deviennent victimes du dilemme :

1. Imaginons que j’ai trois chiens : Fitfit, Foufou et Fiafia. Fitfit, Foufou et Fiafia sont mes deux chiens et chacun a des poils, donc tous mes chiens ont des poils : on a une tautologie. Fitfit et Foufou ont des poils, donc tous mes chiens ont des poils : on a un non sequitur comme on n’a pas vérifié le cas de Fiafia.
2. « En un même lieu et en absence de résistance de l’air, tous les corps ont le même mouvement de chute libre s’effectuant avec la même accélération g, quel que soit le corps pesant. (g est l’accélération de la pesanteur au point considéré.). (source) ». On a là encore un non sequitur car il est impossible d’observer « tous les corps » en chute libre dans le monde sans exception.

La science ne dépend-elle vraiment que de l’induction ?

On peut faire une petite digression sur la science. La plupart des empiristes pensent que la science (les théories scientifiques) est immunisée face à la critique de Stuart Mill contre la déduction car elle repose non sur la déduction mais sur l’induction.

→ D’après le paragraphe précédent, l’induction est invalide si on rejette les universaux, donc la science aussi. De plus, il est faux de dire que la science repose uniquement sur l’induction car elle s’appuie sur des prédictions qui elles utilisent la déduction. En particulier les théories scientifiques formalisées par des formules mathématiques. Les mathématiques sont rappelons-le, la discipline par excellence des déductions.

Exemple d’utilisation du syllogisme en mathématiques

Il n’y a qu’à prendre par exemple le fameux théorème de Pythagore pour le voir :

Si un triangle est rectangle, le carré de la longueur de l’hypoténuse (ou côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés.

Il se reformule facilement sous la forme d’un syllogisme lorsqu’on l’applique à un triangle rectangle précis :

1. Tout triangle rectangle a le carré de la longueur de l’hypoténuse (ou côté opposé à l’angle droit) égal à la somme des carrés des longueurs des deux autres côtés.
2. Le triangle ABC de côtés AB = 5 cm, BC = 3 cm et AC = 12 cm est rectangle.
3. Donc il a le carré de la longueur de son hypoténuse égal à la somme des carrés des longueurs de ses deux autres côtés.

Pour un exemple plus terre à terre, « 2 + 2 = 4 » peut jouer le rôle de la majeure :

1. Si on a deux choses d’un même type et qu’on y ajoute deux choses encore du même type, on obtiendra en tout quatre choses du même type.
2. Ajouter deux pommes à deux pommes, c’est bien ajouter deux choses du même type à deux choses du même type.
3. Donc ajouter deux pommes à deux pommes donnera quatre pommes.

Exemple d’utilisation du syllogisme en sciences (dans les théories scientifiques)

Prenons l’exemple des lois de Newton (notons LN dans la suite) pour comprendre comment les théories scientifiques² utilisent bien la fois l’induction et la déduction (je ferai une grande simplification, mes connaissances en physique étant limitées) :

Induction : étape nécessaire pour trouver la loi générale, le principe universel qui servira à prédire des observations dans le futur. On oppose plusieurs hypothèses (plusieurs principes, théories scientifiques possibles) et on regarde lesquelles sont les plus appuyées par des expériences et des prédictions. La meilleure théorie sera celle qui aura le plus fort pouvoir prédictif (prédire le mieux l’avenir) et qui ne rencontrera pas (ou au moins le moins) d’observations incompatibles.

1. On n’observe pas ou peu de phénomènes incompatibles avec les LN, contrairement à d’autres théories.
2. On voit que les LN prédisent bien le mouvement des ballons (par induction car on a réalisé l’expérience avec plein de ballons).
3. Donc les ballons respectent les LN.
4. On voit que les LN prédisent bien le mouvement des ressorts (par induction car on a réalisé l’expérience avec plein de ressorts).
5. Donc les ressorts respectent les LN.
6. On voit que les LN prédisent bien le mouvement des chiens (par induction car on a réalisé l’expérience avec plein de chiens).
7. Donc les chiens respectent les LN.
8. Etc. (on répète l’expérience avec plein d’autres types d’objets macroscopiques…)
9. Donc, par induction : Tous les objets macroscopiques en général respectent les LN. (principe général)

Il faut cependant préciser que dans le cas des théories scientifiques, le principe général (ici la proposition 8.) n’est pas connue avec certitude mais il est seulement probable (plus que les autres théories scientifiques rivales) qu’elle soit vraie. Toute observation du futur qui tiendrait lieu de contre-exemple pourrait venir l’invalider. Autrement dit, toute théorie scientifique n’est que provisoire, contrairement aux premiers principes qui eux restent vrais en tout temps et ce quel que soit les découvertes que nous ferons.

Déduction : Maintenant que nous avons notre principe général et notre théorie scientifique de validée, nous pouvons l’utiliser pour faire des prédictions grâce à la déduction. On obtiendra nos prédictions grâce à des syllogismes où le principe général que nous avons découvert jouera le rôle de majeure. Par exemple on a de 1. à 3. notre syllogisme pour prouver qu’on peut bien appliquer les LN à moi-même et 4. pour faire des prédictions sur par exemple ma position d’arrivée :

1. Tous les objets (macroscopiques) en général respectent les LN. (principe général)
2. Laurent est un objet macroscopique.
3. Donc Laurent respecte les LN.
4. Donc on peut prédire que Laurent arrivera à cet instant t à cette position précise (x, y, z), etc.

Retour à l’induction et la déduction : pourquoi l’induction tombe aussi face au dilemme « tautologie ou non sequitur » ?

Pour revenir à notre sujet avant cette digression sur la science, voyons pourquoi l’induction, tout comme la déduction, n’est pas épargnée par le dilemme de Stuart Mill. Pour comprendre, il faut saisir l’analogie qu’on peut faire entre induction (lors de la troisième opération de l’esprit) et abstraction (lors de la première opération de l’esprit).

L’abstraction

L’abstraction, c’est le processus par lequel on forme un concept universel dans nos pensées après avoir fait l’expérience d’un certain nombre (suffisant) d’exemples particuliers. Par exemple, on peut comprendre ce qu’est un « homme » ou la « nature humaine » après avoir rencontré plusieurs individus de cette espèce. Plus techniquement, l’abstraction, c’est séparer mentalement l’essence commune et universelle (ce qui est commun à tous les individus d’un même type), ici le fait d’être un animal rationnel, des accidents « individualisants » (qui sont à l’origine des différences entre chaque individus du même type) comme le genre, l’origine ethnique, la taille, l’âge, etc.

L’induction

Tout comme l’abstraction est un pouvoir de l’esprit qui permet de passer de particuliers sensibles à un universel qu’on comprend mentalement (des hommes à l’Homme) lors de la première opération de l’intelligence (la compréhension), l’induction est un pouvoir qui permet de passer de propositions particulières (des rapports de nos observations par les sens) à une proposition universelle lors de la troisième opération de l’intelligence (le raisonnement). Par exemple, c’est passer de « Laurent est mortel », « Maxime est mortel », « Étienne est mortel » et ainsi de suite à « tous les hommes sont mortels ».

Une illustration de l’induction

Kreeft propose un très bon exemple pour comprendre l’induction. C’est l’histoire de deux paysans européens du Moyen Âge qui n’ont jamais bougé de plus de cinq kilomètres au-delà de chez eux. Ils n’ont donc vu que cinq cents êtres humains de toute leur vie.

Un jour, ils voient passer des esclavagistes qui vendent des esclaves d’origine africaine. Le premier paysan (c’est Odo) est plutôt vif d’esprit mais le deuxième (c’est Bozo) plus lent à comprendre. Voici leurs réactions :

Odo : C’est horrible de traiter ces êtres humains comme des animaux !

Bozo : Qu’est-ce que tu racontes ? Ce ne sont pas des hommes mais des animaux, tu vois bien qu’ils ont la peau noire et non blanche ! Il n’y a donc aucun mal à les traiter comme cela.

On peut résumer l’argument d’Odo avec deux syllogismes :

Syllogisme 1 pour montrer qu’enchaîner et vendre des hommes est mauvais :

1. Traiter les hommes comme des animaux est mauvais³.
2. Enchaîner et vendre des hommes, c’est les traiter comme des animaux.
3. Donc enchaîner et vendre des hommes est mauvais.

Syllogisme 2 pour montrer que ces commerçants font une mauvaise action :

• Enchaîner et vendre des hommes est mauvais⁴. (reprise de la conclusion 3.)
• Ces commerçants enchaînent et vendent des hommes.
• Donc ces commerçants font une mauvaise action.

Bozo, rappelons-le est un peu moins doué (un doux euphémisme…), il accepte donc le syllogisme 1 mais rejette le syllogisme 2. Il est d’accord pour dire qu’il est mauvais d’enchaîner et de vendre des hommes. Mais il n’est pas d’accord avec Odo pour dire que ces commerçants font une mauvaise action étant donné qu’il considère malheureusement ces hommes africains comme des animaux. Car pour lui, pour être un homme, il faut être blanc et pas noir, pas jaune…

Pourquoi Bozo se trompe-t-il donc autant ? C’est parce qu’il ne fait pas aussi bien des abstractions qu’Odo. Bozo n’arrive pas à séparer propriétés sensibles stables (avoir deux pieds, deux bras, deux mains, avoir un accent européen, être un homme ou une femme) et propriétés sensibles changeantes (la couleur de peau : blanc, noir, jaune, etc.). Comme tous les humains qu’il a vus étaient blancs et européens, il est évident pour lui qu’il ne peut pas y avoir des hommes différents.

Au contraire, Odo réussit non seulement à abstraire des propriétés sensibles stables comme Bozo mais aussi à abstraire l’essence des accidents parmi ces sensibles stables. Il a compris ce qu’est un homme au plus profond : la capacité à raisonner dans des conditions normales. Ce n’est pas la couleur de peau, l’accent, la taille qui définit un homme.

Voici un schéma quelque peu comique de Kreeft qui résume tout :

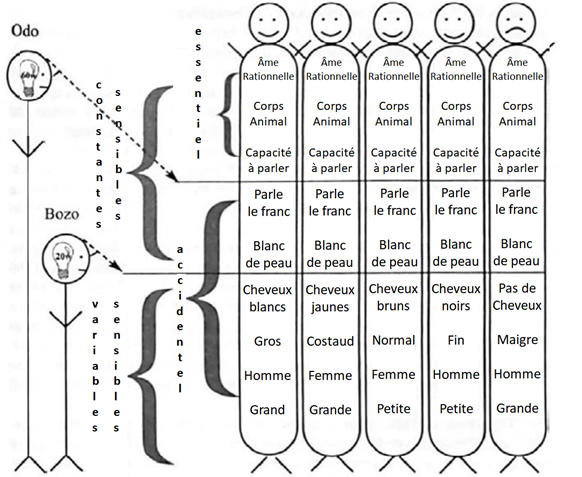
L’exemple de Kreeft illustre bien le fait que l’induction est un raisonnement tout comme la déduction : une opération de l’esprit qui fait intervenir des universaux dans des propositions.

Conclusion : pourquoi l’induction tombe aussi face au dilemme « tautologie ou non sequitur » ?

On peut résumer la réponse par cet argument :

1. Tout raisonnement qui fait intervenir la connaissance d’universaux est invalide (par exemple la déduction) pour les raisons que donne Mill.
2. Or l’induction fait aussi intervenir la connaissance d’universaux.
3. Donc l’induction (tout comme la déduction) est invalide.

---

Illustration de couverture : Charles Laplante, Éducation d’Alexandre par Aristote, gravure, 1866.

1. Kreeft semble penser que l’empirisme mène forcément au nominalisme, mais je ne suis pas convaincu, étant donné cette possibilité.[↩]
2. Je suis conscient des controverses qui battent leur plein en philosophie des sciences ; se pose déjà la question de savoir quels sont les critères pertinents pour discriminer les bonnes des mauvaises théories scientifiques (Karl Popper, Thomas Kuhn, Hempe, etc.). Je reprendrai ceux que personnellement j’ai entendus et appris au lycée. La méthode ressemble à la méthode socratique présentée précédemment.[↩]
3. Sous une forme plus rigoureuse, la forme logique, on aurait quelque chose comme « toute action qui consiste traiter les hommes comme des animaux est mauvaise ».[↩]
4. Sous une forme plus rigoureuse, la forme logique, on aurait quelque chose comme « Toute action qui consiste traiter à enchaîner et à vendre des hommes comme des animaux est mauvaise ».[↩]